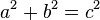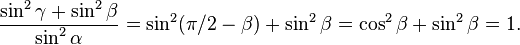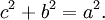Origine [modifica]
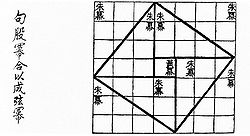
Visualizzazione del caso del triangolo (3,4,5) contenuta nel testo cinese Chou Pei Suan Ching (scritto tra il 200 a.C. e il 200 d.C.)
Enunciato [modifica]
- In ogni triangolo rettangolo, l'area del quadrato costruito sull'ipotenusa è equivalente alla somma delle aree dei quadrati costruiti sui cateti.
Inversamente, ogni triangolo in cui i tre lati verificano questa proprietà è rettangolo: questo teorema, con la sua dimostrazione, appare negli Elementi immediatamente dopo il teorema di Pitagora stesso.
Dimostrazioni [modifica]
La dimostrazione classica del teorema di Pitagora completa il primo libro degli Elementi di Euclide, e ne costituisce il filo conduttore. Dato che richiede il postulato delle parallele, esso non vale nelle geometrie non-euclidee e nella geometria neutrale. Nel testo di Euclide la dimostrazione del teorema è immediatamente preceduta dalla dimostrazione della costruibilità dei quadrati. L'esistenza stessa dei quadrati dipende infatti dal postulato delle parallele e viene meno nelle geometrie non euclidee. Questo aspetto del problema è in genere trascurato nella didattica contemporanea, che tende spesso ad assumere come ovvia l'esistenza dei quadrati.La dimostrazione del teorema di Pitagora consiste nel riempire uno stesso quadrato di lato uguale alla somma dei cateti prima con quattro copie del triangolo rettangolo più il quadrato costruito sull'ipotenusa e poi con quattro copie del triangolo rettangolo più i quadrati costruiti sui cateti, come in figura.
Essendo il teorema uno dei più noti della storia della matematica, ne esistono moltissime dimostrazioni, in totale alcune centinaia, opera di matematici, astronomi, agenti di cambio, una delle quali si deve a Leonardo da Vinci. Questo numero così alto accomuna il teorema di Pitagora a quello della reciprocità quadratica, per il quale sono stati classificati, in circa due secoli, almeno 233 diversi percorsi dimostrativi[2].
Dimostrazione di Perigal [modifica]
Esaminiamone alcune interessanti. Quella proposta nel 1873 dall'agente di cambio Henry Perigal si basa sulla scomposizione del quadrato costruito sul cateto maggiore, in giallo nell'immagine: tagliandolo infatti con due rette passanti per il suo centro, una perpendicolare ed una parallela all'ipotenusa, si può ricomporre in maniera da incorporare l'altro quadrato, e formando il quadrato sull'ipotenusa, come nella figura.Dimostrazione di Airy [modifica]
Esiste anche una dimostrazione in forma poetica, dell'astronomo Sir George Airy, in inglese:- "I am, as you can see, a² + b² - ab When two triangles on me stand, Square of hypothenuse is plann'd But if I stand on them instead The squares of both sides are read."
- "Come potete vedere, sono a² + b² - ab Quando ci sono due triangoli sopra di me È rappresentato il quadrato dell'ipotenusa Ma se invece sto io sopra di loro Si leggono i quadrati dei due lati"
Sia quella di Perigal che quest'ultima sono interessanti, in quanto sono puramente geometriche, ossia non richiedono alcuna definizione di operazioni aritmetiche, ma solo congruenze di aree e di segmenti.
Quadrati concentrici di Pomi [modifica]
Dimostrazione geometrica basata su due quadrati concentrici, di lati rispettivamente pari all'ipotenusa (c) e alla somma dei due cateti (a+b).Come si vede dalla figura, tolti i 4 triangoli rettangoli (in giallo di area (a * b) / 2) al quadrato più grande, che corrisponde all'area (a + b)2, si ottiene il quadrato più piccolo, rappresentato in bianco, che equivale invece all'area c2.
Quindi (a + b)2 − 4 * (a * b) / 2 = c2da sui risolvendo si ottiene : a2 + b2 = c2
Questa dimostrazione ha il vantaggio di avere una rappresentazione visiva semplice e diretta, che non richiede lo spostamento e sovrapposizione di forme come le altre dimostrazioni geometriche formulate.
Dimostrazione di Garfield [modifica]
Un'altra dimostrazione geometrica particolarmente significativa, in quanto nella costruzione non compare alcun quadrato, fu trovata nel 1876 da Garfield, che in seguito divenne il ventesimo Presidente degli Stati Uniti d'America. Allora nell'esercito, Garfield commentò il suo risultato: "Questo è qualcosa su cui i due rami del parlamento potranno essere d'accordo".La dimostrazione è la seguente:
- consideriamo una copia del triangolo rettangolo in questione, ruotata di 90 gradi in modo da allineare i due cateti differenti (nella figura a lato il rosso ed il blu). Si uniscono poi gli estremi delle ipotenuse, e si ottiene un trapezio. Uguagliando l'area del trapezio alla somma di quelle dei tre triangoli retti, si dimostra il teorema.
Una apparente dimostrazione con i numeri complessi [modifica]
Una (apparente) dimostrazione puramente algebrica fa uso dei numeri complessi e della formula di Eulero: siano a, b i cateti e c l'ipotenusa. Se i cateti sono allineati sugli assi, abbiamo- a + ib = ceiθ
- a − ib = ce − iθ
- a2 + b2 = c2
Se infatti si sostituisce all'esponenziale immaginario la sua definizione, l'identità si rivela essere: (cosθ + isenθ)(cosθ − isenθ) = 1, ossia cos2θ + sen2θ = 1
e l'ultima ben nota identità non è altro che una possibile formulazione dell'enunciato del teorema di Pitagora.
(Se invece l'esponenziale immaginario è definito attraverso la somma della sua serie di Taylor, allora il problema diviene quello di dimostrare la relazione a + ib = ceiθ, dove a, b e c sono le misure di cateti e ipotenusa di un triangolo rettangolo: problema la cui soluzione di nuovo non è più semplice di una delle dimostrazioni precedenti del teorema di Pitagora).
Con i teoremi di Euclide [modifica]
Un'altra dimostrazione utilizza il primo teorema di Euclide. Si traccia l'altezza sull'ipotenusa, di lunghezza h. Questa spezza l'ipotenusa in due segmenti, di lunghezza p e q. Il teorema di Euclide fornisce le relazioniInverso [modifica]
Vale anche l'inverso del Teorema di Pitagora (proposizione 48 del primo libro degli Elementi di Euclide): "Se in un triangolo di lati a, b e c vale la relazione a2 + b2 = c2, allora il triangolo è rettangolo".Dimostrazione. Sia T un triangolo di lati a, b e c tale che a2 + b2 = c2. Consideriamo un secondo triangolo rettangolo T' che abbia i cateti pari ad a e b (è sempre possibile costruire un triangolo rettangolo dati i due cateti). Per il Teorema di Pitagora (diretto) l'ipotenusa del triangolo T' sarà pari a
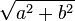 , ossia sarà uguale al lato c del triangolo T. I due triangoli T e T' risulteranno dunque congruenti per il terzo criterio di congruenza, avendo tutti e tre i lati ordinatamente uguali. Ma allora anche il triangolo T sarà rettangolo (CVD).
, ossia sarà uguale al lato c del triangolo T. I due triangoli T e T' risulteranno dunque congruenti per il terzo criterio di congruenza, avendo tutti e tre i lati ordinatamente uguali. Ma allora anche il triangolo T sarà rettangolo (CVD).Applicazioni pratiche dell'enunciato inverso [modifica]
L'enunciato inverso fornisce anche un semplicissimo sistema per costruire un angolo retto (o per controllare la quadratura di un angolo già esistente) in situazioni pratiche, come la topografia o l'agrimensura.A titolo di esempio, con una fune di lunghezza pari alla somma di una terna pitagorica (diciamo 12, somma di 5, 4 e 3, in una qualche unità di misura) sarebbe sufficiente disporre le due porzioni minori della corda (quelle di misura 4 e 3) ad un certo angolo fra loro; se gli estremi della fune, disposta infine in forma triangolare, si chiudono, si saprà che l'angolo compreso fra le due porzioni minori della corda (a questo punto i due cateti) è certamente retto.
Generalizzazioni [modifica]
Il teorema di Pitagora può essere generalizzato in vari modi. Solitamente, una generalizzazione è una relazione che si applica a tutti i triangoli, e che applicata ai triangoli rettangoli risulta essere equivalente al teorema di Pitagora.Teorema del coseno [modifica]
| Per approfondire, vedi la voce Teorema del coseno. |
La generalizzazione più importante del teorema di Pitagora è forse il teorema del coseno, che si applica ad un triangolo qualsiasi (non necessariamente retto). In un triangolo con vertici e angoli indicati come in figura, vale l'uguaglianza:
Teorema dei seni [modifica]
| Per approfondire, vedi la voce Teorema dei seni. |
Il teorema dei seni mette in relazione le lunghezze dei lati di un triangolo e i seni degli angoli opposti. Anche questa relazione si applica a qualsiasi triangolo e, nel caso in cui questo sia rettangolo, può essere ritenuta equivalente al teorema di Pitagora (benché in modo meno immediato rispetto al teorema del coseno).
Il teorema dei seni asserisce che in un triangolo qualsiasi, con le notazioni come in figura, valgono le relazioni seguenti:
Generalizzazione che non fa uso di trigonometria [modifica]
È possibile estendere il teorema di Pitagora ad un triangolo qualsiasi senza fare uso di funzioni trigonometriche quali il seno ed il coseno. Dato un triangolo ABC come in figura, si tracciano due segmenti che collegano il vertice A con due punti g e h contenuti nel segmento opposto BC (oppure in un suo prolungamento), in modo tale che gli angoli AgB e AhC siano entrambi uguali all'angolo α del vertice A. La figura mostra un caso in cui l'angolo α è ottuso: se è acuto, i due punti g e h sono in ordine inverso (il primo a destra e il secondo a sinistra) e possono uscire dal segmento BC.Vale la relazione seguente: